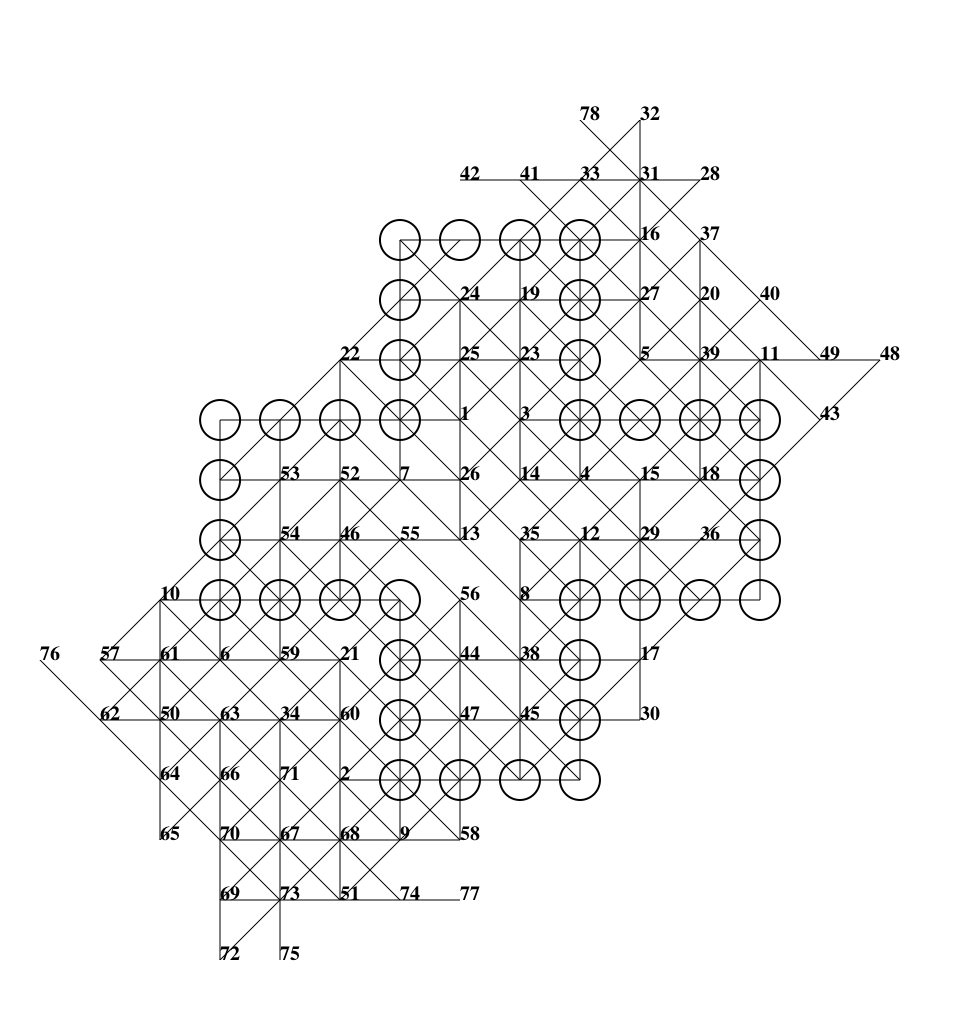
Go down for the high scores (The best solution is now 79).
Here is a game that my father plays from time to time. Try it: it's very simple, and fun when you have nothing else to do. You start with a cross formed by 36 points on a grid as shown below (images were generated by a script from Stefan Schmieta, further improved by Erik D. Demaine):

At each step, add a line in any of the 4 directions : | - / \, passing thru 5 adjacent points of the grid, 4 of which already exists, and one that you add. For example, from the starting position above, you could add a line and obtain:
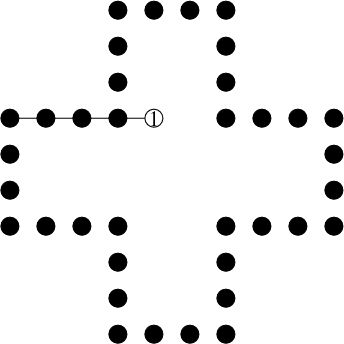
Moreover, two lines in the same direction cannot touch each other, i.e. cannot share a point, and each line has to have exactly five points.
The goal is to draw as many lines as possible.
What is the maximum number of lines you can draw? One can easily find an upper bound of - say - 141, can you prove a better bound?
After several years of intensive search, my father has never been able to exceed 64 lines (see below). Is there a better solution?
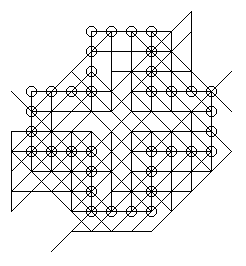
If you can improve those upper and lower bounds of the optimal solution, send me an email, and I'll include your result in this page.
Stefan Schmieta's program found a better solution: the number to beat is now 65
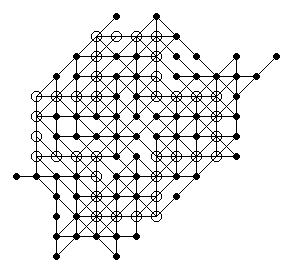
He used a simple random walk algorithm!
Oct 1999
The human mind proved once more its supremacy over the machine (but
for how long??). My dad raised the high score to 67, and then 68.
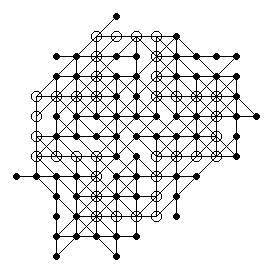
Here is the 68 solution:
Dec 2006
Machines win this new round with a new high score of 69, 72, then 74.
The solutions were constructed by
Heikki Hyyro and
Timo Poranen
using a simulated annealing algorithm.
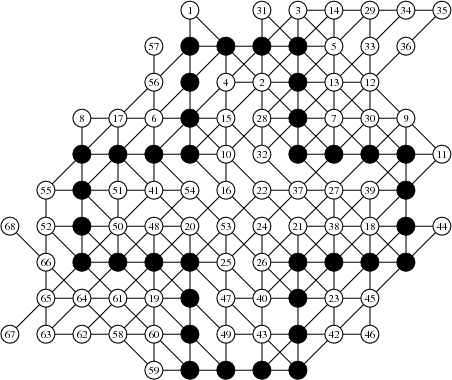
Here is 74 (click for an animated gif, also available in
xfig and
eps).
May 28, 2007
A new record of 76 appears in the paper "Reflexive Monte-Carlo Search" by
Tristan Cazenave
that was recently accepted in CGW 2007 in Amsterdam. He
further improved his result to 78: